در مطالب موجود در سایت یارکد، راه‌های مختلفی برای کاهش میزان داده‌های استفاده شده در نمایش یک تصویر بیان شده است. اما سوالی که در اینجا مطرح می‌شود این است که واقعا چه تعداد بیت برای نمایش اطلاعات یک تصویر کافی است. به عبارت دیگر، کمترین مقدار داد‌ه‌هایی که برای توصیف یک تصویر بدون از دست دادن اطلاعات آن کافی است، چقدر است؟

تئوری اطلاعات یک چهارچوب ریاضی برای پاسخ به این سوال و سوالات مربوطه فراهم می‌کند. قضیه اساسی این تئوری  این است که اطلاعات را می‌توان بصورت یک فرآیند آماری مدل سازی کرد، بطوریکه بتوان آن را بصورتی سازگار با منطق اندازه گیری کرد. در ارتباط با این فرضیه، پیشامد تصادفی E با احتمال وقوع P دارای I واحد اطلاعات است که بصورت زیر قابل محاسبه است:

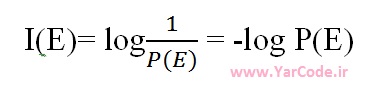
میدانیم که اگر P(E)=1 باشد یعنی رخداد پیشامد E قطعی است. در اینصورت I(E)=0 خواهد شد و بنابراین، بیانگر هیچ اطلاعات مفیدی نیست. از انجایی که هیچ گونه عدم قطعیتی در ارتباط با این پیشامد وجود ندارد، بنابراین دانستن وقوع این پیشامد هیچ اطلاعات جدیدی بدست نمیدهد. مبنای لگاریتم استفاده شده در معادله مطرح شده در بالا مشخص گننده واحد اندازه گیری اطلاعات است. بعنوان نمونه اگر از مبنای 2 استفاده شود، عدد بدست آمده بیانگر میزان اطلاعات در واحد بیت است.

اکنون تصور کنید منبعی از پیشامدهای تصادفی مستقل آماری از یک مجموعه گسسته از پیشامدهای ممکن {a₁,a₂,…,a_j} با احتمالات وقوع {P(a₁),P(a₂),…,P(a_j} در دست باشد، متوسط اطلاعات خروجی منبع مذکور، آنتروپی آن منبع نامیده میشود و مطابق با رابطه زیر تعریف میشود:

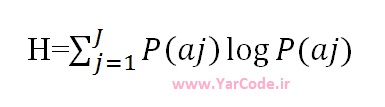
اکنون فرض کنید یک تصویر را بعنوان یک منبع شدت روشنایی فرضی در نظر بگیریم، در این صورت با استفاده از هیستوگرام تصویر، آنتروپی منبع شدت روشنایی چنین تعریف میشود:

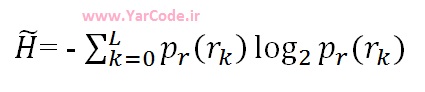
در پایان قابل ذکر است که معادله فوق یک حد پایین برای فشرده سازی قابل حصول به کمک کدگذاری مستقیم پیکسلها به ما ارائه میدهد، اما این معادله دیگر در حالت همبسته بودن پیکسلهای یک تصویر برقرار نیست و میتوان چنین تصویری را با متوسط بیت بر پیکسل کمتری نسبت به معادله مذکور، کدگذاری کرد.

 

این مطلب توسط مهدی مقیمی و به منظور قرارگیری در سایت علمی آموزشی یارکد (YarCode.ir) تهیه شده است.